MDCT
Its really high time to update by blog before it starts rotting. So here are a few words about the modified discrete cosine transform. The reason why iam writing this, is that most docs about the MDCT ive seen are quite obfuscated so i thought maybe i could do better (or worse ;)). Note ive made no attempt to write formal proofs for sake of readability, but they are all very trivial.
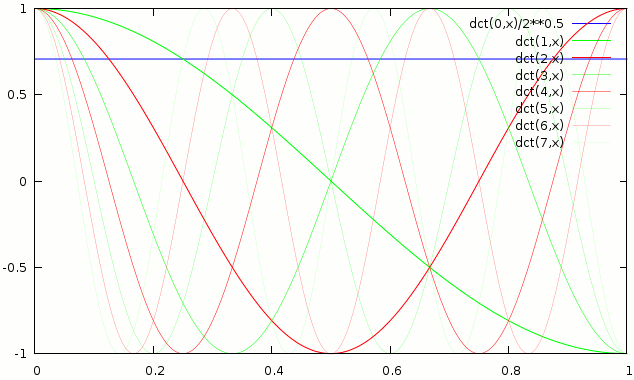
Basis functions of the normal DCT
Basis functions of the MDCT
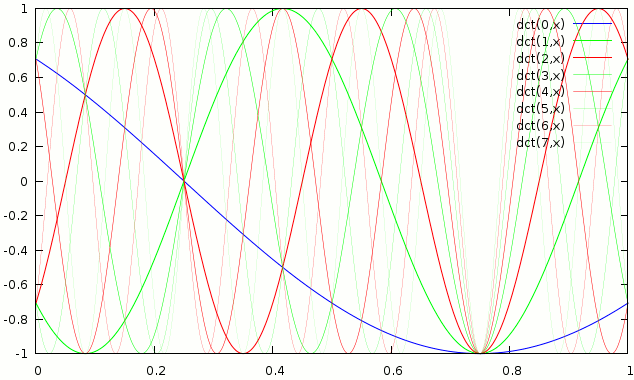
Both of the transforms have orthogonal basis functions, that is the forward transform is simply the series of dot products of the input and the basis functions. While the inverse transform is the sum of the basis functions each scaled by the dot product from the forward transform. This can also be said in a dozen different ways …
What makes the MDCT special, is that it has half as many basis functions as it has inputs. Thus performing the MDCT and then IMDCT on a single block will generally not result in the original. The magic with the MDCT is that it can be overlapped by 50% and then suddenly doing the MDCTs and IMDCTs leads to perfect reconstruction of the original. One can see such lapped transform as a single non lapped transform of infinite length if one wants.
To proof that simply applying the MDCT and then the IMDCT on each block i, which is 50% lapped over block i-1 leads to the original, one really only has to proof that all basis functions are orthogonal (have a mutual dot product = 0). We already assumed that the basis functions of a single MDCT are orthogonal (that can easily be proofen by trigonometric identities if someone is bored). We also know that non adjacent blocks can only have mutually orthogonal basis functions as they do not overlap. Whats left are the adjacent blocks. The proof for their orthogonality is very trivial, if one looks at the graph above, it is immedeatly obvious that there are 2 symmetries one at 0.25 and one at 0.75 in all basis functions. So they behave as (…, c, b, a, -a, -b, -c, …, x, y, z, z, y, x, …). Thus the dot product of 2 basis functions of 2 adjacent blocks is …
… c*x + b*y + a*z – a*z – b*y – c*x … which is obviously 0.
I also should mention that because of these 2 symmetries mentioned above one really just needs to calculate 50% of the IMDCT as the rest is identical up to the sign
The above is still missing one detail, that is that normally the (I)MDCT is used with a window to smoothly get the basis functions down to 0 at their ends. An example with sine window is below
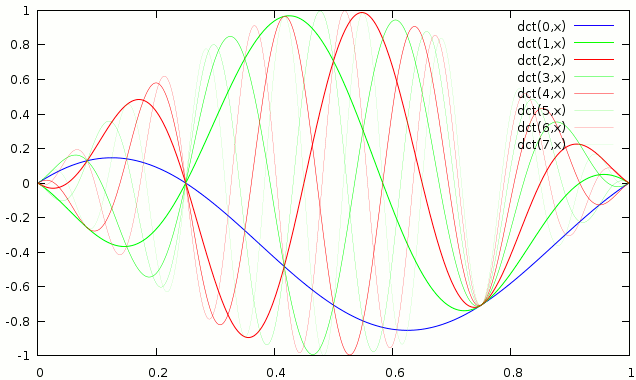
The obvious question is, are the basis functions still orthogonal? The blocks which are not adjacent of course still have to be because their basis functions dont overlap. The basis functions from adjacent blocks assuming a symmetric window
(…c*w-2, b*w-1, a*w0, -a*w1, -b*w2, -c*w3, …, x*w3, y*w2, z*w1, z*w0, y*w-1, x*w-2, …) now have a dot product of …c*w-2*x*w3 + b*w-1*y*w2 + a*w0*z*w1 – a*w1*z*w0 – b*w2*y*w-1 – c*w3*x*w-2 … which is still 0 thus to our “big surprise” any symmetric window maintains orthogonality between 2 adjacent blocks. Whats left are the basis functions within a block. For them the dot product looks like
… c*C*w-22 + b*B*w-12 + a*A*w02 + a*A*w12 + b*B*w22 + c*C*w32 … + x*X*w32 + y*Y*w22 + z*Z*w12 + z*Z*w02 + y*Y*w-12 + x*X*w-22 …
or reordered and common stuff factored out:
… c*C*(w-22+w32) + b*B*(w-12+w22) + a*A*(w02+ w12) +
… x*X*(w32+w-22) + y*Y*(w22+w-12) + z*Z*(w12 + w02)
If we now choose a window for which wi2 + w1-i2 = 2 then the dot product equals what it is without the window, thus our windowed MDCT is still orthogonal and thus easy invertible
One thing that could be of interest is that the analysis window and the syntheis window doesn’t have to be the same. http://research.microsoft.com/~malvar/papers/dfsp98.pdf page 2 describes the requirement for perfect reconstruction in that case. Atrac3 uses this, (most likely atrac3+ also).
Comment by Benjamin Larsson — 2008-06-09 @ 11:03
Also possibly worthy of note for readers of this post – I’m lead to believe that FFmpeg dsputil (I)MDCT routines calculate 100% of the data, not taking advantage of symmetries, they use ‘radix 2’ when ‘radix 4’ would fit into SSE registers and if all code using the (I)MDCT routines is edited, a reordering phase can be avoided all leading to performance improvements. I’m not very familiar with this they’re just notes upon which I have stumbled during my travels so please make corrections. :) Hopefully someone will be motivated to pick this up and improve FFmpeg.
Comment by Robert Swain — 2008-06-17 @ 00:54
FFmpeg’s imdct does exploit the 2x symmetry. Split radix is a different optimization. And radix is independent of register size.
Reordering can’t be removed in general. Unlike video codecs where the dct permutation can be included in the zigzag, audio codecs don’t inherently have any permutation, so if your transform needs one you have to add it somewhere. At best you can save some memory accesses by merging reorder into bitstream parsing; at worst that might be slower depending on how the entropy coder works (e.g. vorbis does multiple passes over the coefs).
Comment by Anonymous — 2008-06-29 @ 09:44
> FFmpeg’s imdct does exploit the 2x symmetry.
Well, ffmpegs imdct outputs twice as many values as needed, thats a waste of memory writes and subsequent reads, as well as cache space at least. CPUs are quite a bit faster than memory so this could have a bigger effect on speed than what it looks like …
Comment by Michael — 2008-06-29 @ 14:30
I have learn a few good stuff here. Definitely price bookmarking for revisiting.
I wonder how a lot effort you place to create this sort of great informative
web site.
Comment by เà¸à¸¡à¸¡à¸¹à¸£à¹ˆà¸² — 2015-06-20 @ 03:39
the description provided above is simply superb……….
Comment by Anonymous — 2015-09-08 @ 07:41
What’s Going down i aam new to this, I stumbled upon this I have found It absolutely helpful and it has helped me
out loads. I am hoping to give a contribution & help other users like its aided me.
Great job.
Comment by comment devenir riche sur internet — 2015-11-28 @ 17:53
Right here is the perfect webpage for anyone who would like to find out
about this topic. You realize a whole lot its almost tough to argue
with you (not that I really will need to…HaHa). You certainly
put a fresh spin on a subject that’s been discussed foor many years.Excellent stuff, just excellent!
Comment by dépenser moins — 2016-07-07 @ 17:21