Lair Of The Multimedia Guru

If you looked into a modern acer notebook (i bought mine in 2025-09), you will see thick black stickers on many components, like the NVME SSD and SO-DIMM modules.
You may wonder why your SSD reached about 108°C (with and without the sticker) and the unmodified stock SO-DIMM 87°C with the sticker, with ambient air temperature of 26°C. Well dont ask me, iam wondering too.
And why the SSD is roughly 20°C cooler with a random noname 2mm thick heatsink with little airflow, as it touches the bottom cover.

Lets find out, lets test these stickers :)
What we will do here, is heat one of these stickers and a thin aluminium heatsink side by side up on one end, and using an IR camera and my fingers measure how well it conducts heat.

Left is a noname chinese aluminium heatsink, right is the acer black sticker. The precision laboratory hot plate used is at 108°C, the sticker on the outer side per IR camera is 31.4°C and is cool to the touch on the outer side. The heatsink is too hot to touch, aka it hurts if i touch it. The IR camera measures the outer part of the heatsink at 94.7°C

Why is acer putting these fake heat-spreader stickers on the components ?

Ive seen many fireflies in teh woods in the last days, wondered if they can be filmed. When i search for firefly video, 100% of results is fake and computer generated.
Was in the woods yesterday and took 2 videos (Fireflies video1 and Fireflies video2) from the fireflies there. So quite doable, iam sure one can do better than me on my first try. Used a canon m100 with a old viltrox EF-EOS M2 x0.71 Adapter a EOS-M42 Adapter and a Asahi Opt Co. Super Takumar 50/1.4 I got that lens for free on a old spotmatic camera for maybe 50€ really long ago. Feel free to use the 2 videos as you see fit as long as you give me credit.

Whats the fastest approximation of log2() ?
simply reading a floating point value as if it was the corresponding integer. Strictly in C one of course has to use union not a cast to avoid undefined behavior. But the operation is better described by casting a pointer from type *float to *int32_t. The same works with double and int64_t
Its actually quite accurate:

// for all the int2foat / float2int stuff please see: https://git.ffmpeg.org/gitweb/ffmpeg.git/blob/HEAD:/libavutil/intfloat.h

    for (int64_t i = -0x7FFFFFFF; i < 0x7FFFFFFF; i+= 1<<20) {
        float f = av_int2float(i);
        float exact = log2f(f);
        float approx = ((float)av_float2int(  f)     - 0x3F800000) / (1<<23);
        float approx2= ((float)av_float2int(f*f)     - 0x3F800000) / (1<<24);
        float approx4= ((float)av_float2int(f*f*f*f) - 0x3F800000) / (1<<25);
        printf("x = %12e exact = %12.5f approx = %12.5f err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f,\n",
               f, exact, approx, approx - exact, (approx - exact) / exact,
               approx2 - exact, (approx2 - exact) / exact,
               approx4 - exact, (approx4 - exact) / exact
              );
    }

// for all the int2foat / float2int stuff please see: https://git.ffmpeg.org/gitweb/ffmpeg.git/blob/HEAD:/libavutil/intfloat.h

    for (int64_t i = -0x7FFFFFFFFFFFFFFF; i < 0x7FFEFFFFFFFFFFFF; i+= 1LL<<48) {
        double f = av_int2double(i);
        double exact = log2(f);
        double approx = ((double)av_double2int(  f)     - 0x3FF0000000000000) / (1LL<<52);
        double approx2= ((double)av_double2int(f*f)     - 0x3FF0000000000000) / (1LL<<53);
        double approx4= ((double)av_double2int(f*f*f*f) - 0x3FF0000000000000) / (1LL<<54);
        printf("x = %12e exact = %12.5f approx = %12.5f err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f,\n",
               f, exact, approx, approx - exact, (approx - exact) / exact,
               approx2 - exact, (approx2 - exact) / exact,
               approx4 - exact, (approx4 - exact) / exact
              );
    }

You can also improve the precision further by squaring the argument and dividing the result by 2, this reduces the range though each time.
The tiny spot of divergence at the very left are caused by the subnormal numbers.

Ubuntu 20.04 soon will be unsupported outside ESM so i thought, ill just upgrade that
one box quickly theres little special on it, it should go smoothly. This box is not
critical either. It all looked good until snap was updated.
That simply errored out, apparently it wanted to connect to the network in the middle
of the upgrade (not ok).

But why did the network connection fail ?
ubuntu upgraded unbound, fucked the config up and while i had seen the note about it,
i thought yeah ill fix it later if it breaks. But whatever, i fix that one include line
in the config and restart unbound and that fixes it.
And then we restart do-release-upgrade, but that refuses to continue.
So we just run apt-get dist-upgrade and that happily finishes with no issues.
We confirm that everything points to the new distro version and no broken packages remain
all good, ohh boy i was wrong

After a reboot the system had lost its graphical desktop environment.
But who cares, ill just do a “apt-get install ubuntu-desktop-minimal” thats gonna fix it
But something was wrong, the list of packages we where missing was really long, this system had a fully
working desktop environment before the upgrade. Anyway i ok-ed the list and expected it would
all be fine in a few minutes. But no, apt couldnt actually install anything, it had no network
access. So i though yeah right lets restart unbound, but no unbound refused to start there was
no network interface. ubuntu had nicely uninstalled all parts of NetworkManager during the “upgrade”
without replacement.

Back to basics, i setup the network old style through /etc/network/interfaces
then installed ubuntu-desktop-minimal which also pulled in NetworkManager
and everything looked good, i rebooted and i was greeted with a blurry GUI luuking
like iam 20 years in the past. Changing resolution, no, thats not it.
the internet hinted to “ubuntu-drivers install” which again failed with no network
so i redid /etc/network/interfaces and retried which without asking installed a bunch of
random drivers (not ok, ubuntu), a reboot later teh GUI looked normal.

And the network again still did not work. The network manager applet wasnt running, the
network did not show up in any GUI, the nmcli said unmanaged. i undid all my stuff from
/etc/interfaces, rebooted and restarted stuff but i couldnt figure out what the correct
way is that ubuntu uses to make this work. The internet also was not revealing about
this, everyone was just hacking around it when they hit this. Theres a config file in
/usr/lib/NetworkManager/conf.d/10-globally-managed-devices.conf
which disabled all ethernet interfaces. And the only way i could make that work was
to override it in /etc/NetworkManager/, then it works but obviously thats not how
ubuntu does it, so thats slightly strange but it works and its just one line so
it seemed not justified to investigate that further.

Anyway, ubuntu reminded me why i hate upgrading these boxes.
Btw, why did this likely happen ? likely i uninstalled some spyware from ubuntu and
ubuntu-desktop-minimal dependent on that which caused ubuntu-desktop-minimal to be
removed with the spyware. And when you upgrade without the ubuntu-desktop-minimal
metapackage then ubuntu messes up upgrading a desktop. But thats just a hypothesis

Update 2025-03-17: Updated that box from 22.04 to 24.04 and surprisingly no problems

With blockchains making sure the transaction you sign is what you wanted to sign is critical.

So professionals use a multi signature gnosis safe … (which is a webapp in the WEB BROWSER) to build a transaction. Then verify it by looking at said WEB BROWSER. And then have multiple independant people with hardware wallets BLINDLY sign this transaction. The used hardware wallets are NOT able to display any details about the signed transaction.

What could possibly go wrong? (we are all safe if we just dont do anything except using these computers with WEB BROWSERS to sign transactions, right?)
ohh lazarus stole 1.5 billion $ from bybit 5 days ago. How could that happen ? They used gnosis safe, they used the best hardware wallets. Alot of details still arent known but oddly enough gnosis safe website seems not fully working even today.

But seriously, why is a “WEB BROWSER” not ok ? Its too complex, it can do too many things, your computer is to complex it can do too many things. You need a minimal piece of hardware and software with minimal features, no execution of remotely downloaded code, no trust of remotely provided information, … if you want security. Hardware wallets that directly do multisig and directly display what is transferred and where to would be an option. (A ledger that you are forced to update regularly through a WEB BROWSER like application and that is closed source and that now even has the official ability to extract the private key is just the next rusty link in the chain of “security”)

Update 2025-02-28: If someone is looking for a hw wallet that supports displaying safe multisig transactions it seems the Keystone wallet can do this.

Update 2025-03-07: Investigation Updates and Community Call to Action

I think this one is just funny, but iam not sure its funny for non geeks/non math people

I had a few minutes time and so i tried asking chatgpt some question about factorials. Iam impressed by chatgpt but then again, iam not.
It could point me to stirlings approximation and the extended variant but then the extended variant with few terms is not the best approximation for its complexity. And lets rather not look at chatgpts explanation why mine performed better.

Just 18 days ago I asked if chi is a ponzi?. Today we seem to have gotten an answer:

Intro

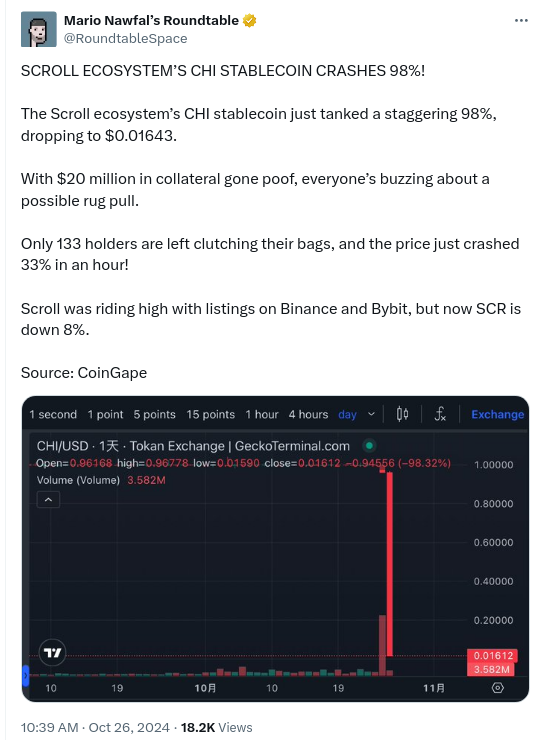
A while ago on some random place, someone mentioned chi as being a great way to make money. Obviously things that are recommended on random places tend to be great ways to loose money. But somehow it made me curious in what way exactly, so i made a note. And a few weeks later i actually found some time to look around what chi is. I will in this text omit several links as i dont want to drive anyone by mistake to it and also nothing here is investment advice. And also i have no position in chi for the record, obviously.

So what is chi?

Chi is a stable coin on the scroll blockchain. It initially was apparently backed by USDC.
This stable coin is mainly tradable on the tokan decentralized exchange. That exchange has a governance token called
TKN and chi has a governance token called ZEN.

What about tokan ?

Tokan exchange works like many DEXes, people provide liquidity and get payed in the exchanges governance token TKN for that.
Others can then use that liquidity and pay fees to trade. So the value of TKN is key to how much
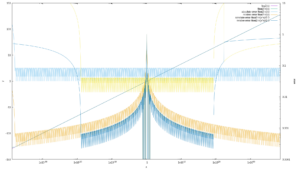
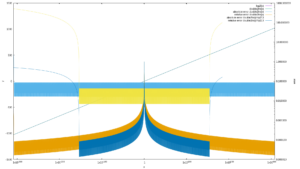
rewards liquidity providers receive. The biggest LP pair is USDC/CHI with 58M US$ value paying over 66% annualized interest. These numbers of course change every minute.

Now normally these DEXes have rapidly droping interest rates and their governance token drops in value as they use up any funding they have. And then normalize on some low interest rate based on fees that traders pay. But this one here is different, if you lookup TKN, as of today its price goes up exponentially, that shouldnt be.

So where does ultimately the money for the interest come from?

It comes from chi being minted and used to buy TKN, propping up the price of TKN. This way the TKN price goes up, and the interest rate for liquidity providers stays high as they are paid in TKN. But the careful reader probably already realized the issue here. The minted Chi is not backed by USD and it goes out in circulation, so someone could decide to redeem it for its supposed value of 1US$ per 1CHI. Really funnily someone even setup a dune page to track the CHI being minted and used to buy TKN

So if we simplify this a bit, basically the money backing CHI is used to pay out the high interest rate and this works as long as enough new people join and not too many leave. Do we have a ponzi here ? You decide.

How bad is it ? Well the people behind chi are funnily actually showing that in their analytics page, you just have to explain what each field really is.

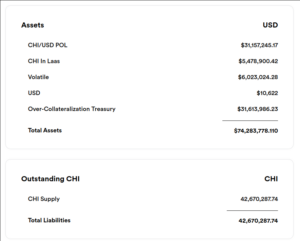
So lets explain what these are, CHI Supply of 42 670 287 is the amount of CHI in existence, some of that are owned by the protocol.
And of today evening compared to morning, theres 4% more, this is rapidly growing.

CHI/USD POL is the USDC+CHI part of the USDC/CHI LP on Tokan that is owned by the protocol. “POL” might be Pool with a typo. This is valid
collateral, the CHI of it can be subtracted from teh CHI Supply and the USDC of it can be used to refund
CHI holders.

CHI In Laas is the CHI part of CHI/ZEN and CHI/TKN LPs on Tokan that is owned by the protocol. This is murky
as a collateral because it only has value if its withdrawn before a bank run happens.
Laas stands for liquidity as a service, in case you wonder.

Volatile and “Over-Collateralization Treasury” are TKN tokens owned by the protocol, they are not usable as collateral, and this is where the real problem starts.

You can look at the “oracle” contract to get these values too and also see from it what each part is.

What would happen if people try to redeem their CHI for US$?

First, lets pick the best case scenario where we assume the protocol can pull all their assets from the DEX before people try to exit. Also keep in mind that i am using the current values of everything and at another time things will be different.
Here first 31.157M/2(CHI part of the USDC/CHI LP) + 5.478M(CHI of laas) that is 21M of 42.6M are owned by the protocol and we just remove them. Leaving
21.6M CHI owned by users that may want to redeem. The protocol now has the USDC part of their USDC/CHI LP left thats 31.157M/2.
that leaves 6M CHI backed by TKN, while on paper these TKN would have a value of over 37M$. As soon as one starts selling
them, they are going to collapse because basically nothing is backing them, the 2 LAAS positions would be already be
used to reduce the amount that needs to be redeemed. Only about 1M$ remains in eth/tkn that one could use to change tkn into
something of value. So basically In this scenario over 5M$ are missing.
If OTOH the protocol does not pull the LAAS pairs before and they are used by people to trade in their TKN and ZEN into CHI
then the circulating supply of CHI that needs to be redeemed could increase by that amount approaching ~10M $ of missing money.
So ATM basically between a quarter and half of the user owned value behind the chi stable coin seems to not exist anymore.

Is a collapse inevitable ?

No, you can have 100 people owning 1 shared US$ and as long as no one takes that 1 US$, everyone can live happy believing they each have 1 US$. Its also possible someone walks up to the box and adds 99$. This is crypto its not impossible someone just pulls 6M$ out of their hat and fixes this hole. But then again, given that the hole becomes bigger every day and the rate by which it grows also grows. I don’t know. I guess ill just hope that all the people are correct, who believe that sticking money into a box will allow everyone to have 66% more each year. Money can be made like that by the central bank or by government bonds or by companies selling a product. But not by wrapping US$ into a funny coin and then providing liquidity between said coin and US$. A coin that seems to have little other use than that.

Ive yesterday updated a 20.04 LTS ubuntu to 22.04. I expected it to just work but do-release-upgrade failed with something like
“The upgrade has aborted. The upgrade needs a total of 6XY M free space on disk ‘/boot’.”
Thats not nice of ubuntu considering the default /boot/ partition size was 500 M when this system was originally setup (i know because i know i left the default).
This system was also setup with disk encryption so simply resizing the partition is not as obvious and simple, not saying it cannot be done, just saying i felt more comfortable with making the update work with 500M /boot than trying to resize it.

So heres a list of solutions. For everyone who runs in this same issue. But before this a few words of caution.
Make a backup or have plan that you LIKE if it goes wrong.
The ubuntu tool is SHIT and this is polite. Its computation of needed space is at best a guess, it simply takes the current kernel size and the current initrd.img sizes and multiplies them by how many are expected to be needed and then asks for free space accordingly. Every number here is wrong. Its not using the actual kernel or initrd sizes, it doesnt use the current compression settings, it doesnt even seem to consider that the currently installed kernels will be removed. In practice for me it overestimated by 156mb but I think it can in corner cases also underestimate the needed space.

• Use your favorite partition resize tool, IFF you can.
• set /etc/initramfs-tools/initramfs.conf: COMPRESS to lzma (xz is slightly worse)
  then run update-initramfs -u, and remember ubuntu (no idea if others will too) will try to change this setting back during the update (it will ask) if you let it, and it changes it back then you may need more space during the update than what the tool computed
• uninstall all but one kernel
• uninstall anything you can from /boot/ like memtest
• Have the one installed kernel be the default standard not HWE in ubuntu IFF your system works with it. Why? its smaller and because if you use a HWE kernel then after the update you will have the current standard, previous standard and HWE kernels on /boot on ubuntu (I have not tested it but i ended with these 3 and i started with just the HWE one, assuming that was because HWE -> HWE + 2xstandard)
• If after all above you still dont have enough space but you are sure you actually have enough space, heres the sketchy solution, set MODULES=dep, run update-initramfs -u set MODULES back to most, run do-release-upgrade
  I did this, it worked for me. But what it effectively does is building a smaller initrd temporary to compensate ubuntus massive space overestimation. For me before, it asked still for around 360-370M free space which was 6M more than i had. In reality whenever i looked during the update there was 156+M remaining free space. You can also try to leave MODULES=dep during the upgrade if you are confident that the system will boot with that and the new kernel or maybe leave it at dep during the upgrade but just before rebooting set it back, removing unneeded kernels and running update-initramfs -u
• If something goes wrong and you run out of space and ubuntu sends you back to the command line (this didnt happen to me) simply try uninstalling some of the extra unneeded kernels with apt remove and do a apt -f install and apt update && apt dist-upgrade, If you have luck that might fix it
• Buy a new disk, install a new OS from scratch (that was my plan if what i did, didnt work)