Lair Of The Multimedia Guru

Whats the fastest approximation of log2() ?
simply reading a floating point value as if it was the corresponding integer. Strictly in C one of course has to use union not a cast to avoid undefined behavior. But the operation is better described by casting a pointer from type *float to *int32_t. The same works with double and int64_t
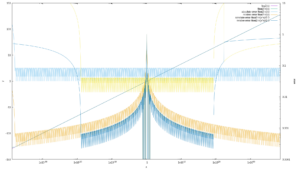
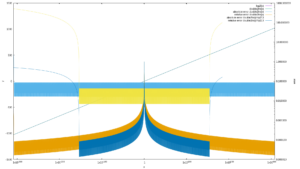
Its actually quite accurate:

// for all the int2foat / float2int stuff please see: https://git.ffmpeg.org/gitweb/ffmpeg.git/blob/HEAD:/libavutil/intfloat.h

    for (int64_t i = -0x7FFFFFFF; i < 0x7FFFFFFF; i+= 1<<20) {
        float f = av_int2float(i);
        float exact = log2f(f);
        float approx = ((float)av_float2int(  f)     - 0x3F800000) / (1<<23);
        float approx2= ((float)av_float2int(f*f)     - 0x3F800000) / (1<<24);
        float approx4= ((float)av_float2int(f*f*f*f) - 0x3F800000) / (1<<25);
        printf("x = %12e exact = %12.5f approx = %12.5f err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f,\n",
               f, exact, approx, approx - exact, (approx - exact) / exact,
               approx2 - exact, (approx2 - exact) / exact,
               approx4 - exact, (approx4 - exact) / exact
              );
    }

// for all the int2foat / float2int stuff please see: https://git.ffmpeg.org/gitweb/ffmpeg.git/blob/HEAD:/libavutil/intfloat.h

    for (int64_t i = -0x7FFFFFFFFFFFFFFF; i < 0x7FFEFFFFFFFFFFFF; i+= 1LL<<48) {
        double f = av_int2double(i);
        double exact = log2(f);
        double approx = ((double)av_double2int(  f)     - 0x3FF0000000000000) / (1LL<<52);
        double approx2= ((double)av_double2int(f*f)     - 0x3FF0000000000000) / (1LL<<53);
        double approx4= ((double)av_double2int(f*f*f*f) - 0x3FF0000000000000) / (1LL<<54);
        printf("x = %12e exact = %12.5f approx = %12.5f err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f, err = %12.5f rel_err= %12.7f,\n",
               f, exact, approx, approx - exact, (approx - exact) / exact,
               approx2 - exact, (approx2 - exact) / exact,
               approx4 - exact, (approx4 - exact) / exact
              );
    }

You can also improve the precision further by squaring the argument and dividing the result by 2, this reduces the range though each time.
The tiny spot of divergence at the very left are caused by the subnormal numbers.